A.D.Walsh published the research work for prediction of geometry of various molecules. It can also be said as a simplest analysis to show connection between Molecular Orbital Theory and Molecular Geometries.
Walsh first of all assumed any confirmation, between two limiting confirmations, to study the co-relation of molecular orbital of one limiting confirmation with those of the other and draw a co-relation diagram. He actually calculated the energies of molecular orbital of reference geometry and its several distortions for simple tri atomic molecules, like water H2O. By plotting a graph between calculated energy of molecular orbital of reference geometry and those of the distorted geometry of a molecule Vs distortion parameter i.e., Bond Angle. Such graph is known as Walsh Diagram.
“Diagram between distorted and reference geometry or energy is called Walsh Diagram”
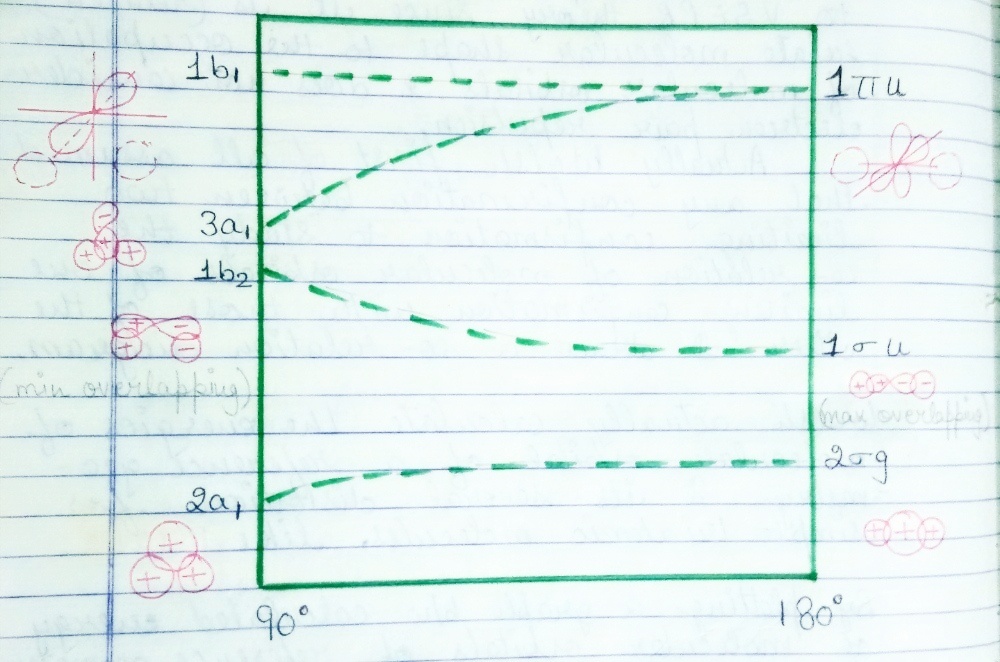
For a linear geometry as AH2 (H2O) tri atomic molecule, the lowest energy value molecular orbital 2σg is formed by s-orbital of A and 1s-orbital of H-atom. On bending the molecule 2a1 orbital forms a slightly lower orbital in energy than the originally 2σg orbitals, This is due to the fact that 1s orbital of H-atom energy is better with each-other and with p-orbital of A on the two fold molecular axis.
The 1σu molecular orbitl of the linear molecule is formed from the p-orbitl of A-atom on the molecular axis and the asymmetric combination of 1s orbital of H-atom. On bending the molecule converts this molecule orbital to 1b2 molecular orbital. This orbital has high energy because 1s orbital do not overlap as well with the p-orbital.
The energy level of doubly degenerate 1πu orbital is highest. It consist the two p-orbitals of A-atom perpendicular to the molecular axis. It does not overlap 1s orbital of H-atom. On bending, the p-orbital which lies on the two fold molecular axis overlap the symmetrical combination of H-1s orbital and then form the 3a1 orbital. This orbital has lower energy than 1πu orbital. It is interesting to note the fall of energy of 3a1 than 1πu is faster than the rise of energy of 1b2 than 1σu. This difference can be explained as on bending the molecule the overlap integral of 3a1 is greater than the decrease in the overlap integral on going from 1b2 to 1σu. At the same time since the p-orbital perpendicular to the molecular plane 1b1 has no overlap in with the H-1s orbital. Hence 1b1 has the same energy as 1πu.
Since in this fig. nucleus-nucleus repulsion and electron-electron repulsion have not been considered. It can be used to predict approximate shapes of the molecule i.e. whether a molecule is Linear or Bent.
Let us consider the molecule BeH2. It has only 4 valence electrons which have lowest 2-orbitals filled. It is clear from the figure that the minimum energy will be achieved by having a linear molecule with 2σg and 1σu. On the other hand the first excited state of BH2 sholud be bent corresponding to 1electron. similarly we can consider CH2 molecule. It has 6 valence electron. It is a bent molecule, from the diagram the bond angle cannot be predicted. Even if bond angle may be calculated which is nearly 134⁰. At this 3a1 and 1b1 energy levels are so close together that the energy difference is less than the repulsion energy between electrons of 3a1 orbital. Therefore the ground state is triplet and electronic configuration is 2a12 , 1b22, 3a11, 1b11.
In case of water (H2O) molecule there are 8 valence electrons 2a12 , 1b22, 3a12, 1b12. Due to steepness of 3a1, 1πu molecule with 5-8 valence electrons water molecule has a bent geometry like CH2.
In general AS2 molecule (tri atomic having 5-8 valence electrons) is predicted to be angular. The observed bond angles are as follows:
BeH2 = 180⁰ CH2 = 134⁰ H2O = 105⁰
BH2 = 131⁰ NH3 = 103⁰

A Walsh diagram is in fact just a more elaborate version of the correlation diagram.

